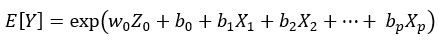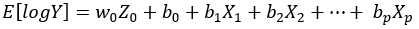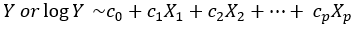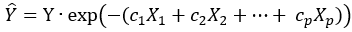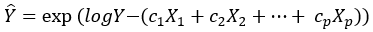Introduction
The purpose of scaling is to remove the variation of response that is described by certain nuisance experimental factors, meaning that scaling can also be called removal of unwanted variation. To distinguish scaling from similarly named procedures such as RUV normalization [1] it is important to keep in mind the following two points. First, the experimental factors participating in scaling are always known (observed) before the model is fitted.
Second, it is important to understand why scaling needs to be performed as a separate step. In the context of single cell analysis, scaled data are meant to be used for subpopulation identification. We assume that the response variance is explained by an unobserved (latent) factor of interest that identifies the subpopulations and by some observed nuisance factor(s). If we perform clustering on unscaled data, it is possible that the data will cluster by the nuisance factor as opposed to the factor of interest. We can compare this to a bulk-RNA experiment where both the factor of interest and the nuisance factors are known and the goal is to find features that are deferentially expressed with respect to the factor of interest. In that case, a separate scaling task is not necessary because we can simply include all of the factors in the model and specify the contrasts only with respect to the factor of interest. Therefore, if for some reason we assume that all of the factors are observed we should skip scaling and apply a bulk-RNA type of differential expression analysis.
Note also that after the k cell types have been identified one can add the corresponding factor with k levels to the data, and the new factor can be treated as observed [3] in downstream analysis.
Model Statement
We assume that for a given single feature (gene) the expected response can be represented as follows:
Here, Equation 1 corresponds to a generalized linear model (Poisson, Negative Binomial, etc) and Equation 2 is loglinear (Lognormal) model. Factor Z0 is the unobserved factor of interest and X1,… Xp are the observed nuisance factors. Because we assume that the library sizes have been already adjusted for via normalization, the intercept term b0 is the same across libraries and no “offset term” (denoted by O in [1], Equation 1) is necessary.
The idea of scaling is to adjust the observed response, Y, so that its expectation is not dependent on X1,… Xp. If a random factor is present in the model, it describes not the expected value of Y but the variance of error term and/or correlation among observations. We treat all of the nuisance factors as fixed because our primary goal is to adjust the expectation of response. However, since in some models (Poisson, Negative Binomial) the response variance is dependent on the mean, we also adjust the response variance for the batch effect whenever such models are used.
We fit a generalized linear or loglinear model with X1,… Xp as covariates to obtain the estimates of c1,… cp as follows:
The values of c1,… cp will coincide with b1,… bp only if Z0 is perfectly independent of X1,… Xp which is never the case in practice. The point is that if we scale the observed Y as follows:
via a generalized linear (Equation 4) or loglinear (Equation 5) model, then the expected value of scaled response, becomes independent of X1,… Xp. If we regress on X1,… Xp we should see far greater p-values than in (Equation 3).
If there is correlation between the nuisance factor and the factor of interest, then by adjusting the response for X1,… Xp, we also reduce its dependence on Z0. The analysis can still be insightful, but only if the factor of interest explains a sizeable part of response variation even after the nuisance factor is taken into account. For a single cell subpopulation study, if there are no meaningful clusters in the end, it might be because there are no distinct cell types, or the distinct cell types are present but the type factor is too correlated with the nuisance factor(s), or a combination of these two scenarios is in play.
Model selection
The scaling step in Seurat [2] allows the user to choose among log-linear, Negative Binomial, and Poisson models. Unfortunately for the user, Seurat provides no guidance as to how to pick the best option and, most likely, the log-linear default is applied all the time in practice. Likewise, if there are a few batch factors, there is no guidance in Seurat as to how to decide what design (a set of batch factors, possibly with interactions) is the best. In particular, including factors that do not exhibit a significant batch effect can lead to overcorrection meaning that the variation of interest is removed instead of the nuisance variation.
In theory, the problem of choosing the best model is tricky because, strictly speaking, the choice of best response distribution is dependent on the unknown factor Z0. That being said, it is possible to automate the model choice by utilizing the AICc exactly the way it is already implemented in Flow GSA. The multiple models are constructed by combining the available response distributions with a set of all possible batch designs up to 2nd order (subject to a hierarchical restriction). In the case of multimodel approach, the final scaled response is obtained by weighting from individual models by the corresponding Akaike weights.
References
[1] Risso et al, 2014, Normalization of RNA-Seq data using factor analysis
[2] Satija et al, 2017 Seurat - Guided Clustering Tutorial, “Scaling the data and removing unwanted sources of variation” section (http://satijalab.org/seurat/pbmc3k_tutorial.html)
[3] Satija et al, 2017 Seurat - Guided Clustering Tutorial, “Finding differentially expressed genes (cluster biomarkers)” section (http://satijalab.org/seurat/pbmc3k_tutorial.html)
Additional Assistance
If you need additional assistance, please visit our support page to submit a help ticket or find phone numbers for regional support.


| Your Rating: |
    
|
Results: |
    
|
32 | rates |