Introduction

Gene-specific analysis (GSA) is a statistical modeling approach used to test for differential expression of genes or transcripts in Partek Flow. The terms "gene", "transcript" and "feature" are used interchangeably below. The goal of GSA is to identify a statistical model that is the best for a specific transcript, and then use the best model to test for differential expression.

Overview of GSA methodology

To test for differential expression, a typical approach is to pick a certain parametric model that can deliver p-values for the factors of interest. Each parametric model is defined by two components:

1. The choice of response distribution, e.g. Lognormal, Poisson, Negative Binomial.
    
2. The choice of model design, i.e. the factors and factor interactions that should be present in the model. Apart from the factor(s) of interest, it might be necessary to include some nuisance factors in order to increase the statistical power of detecting the effect(s) of interest. It is not known in advance which nuisance factors are important enough to be included in the model.

A fairly typical approach is to select the response distribution in advance, regardless of a particular dataset, and assume that the same response distribution is a good fit for all transcripts. GSA provides a more flexible approach by assuming that the transcript expression can be described by the transcript-specific combination of response distribution and design.

For instance, it might be the case that Poisson distribution is a good fit for Transcript 1, but Negative Binomial is a much better choice for Transcript 2. Likewise, the expression of Transcript 1 can be affected by a factor describing the subject's gender, whereas the expression of Transcript 2 is not gender-sensitive.

In GSA, the data are used to choose the best model for each transcript. Then, the best model produces p-values, fold change estimates, and other measures of importance for the factor(s) of interest.

Figure 1. GSA Advanced Options

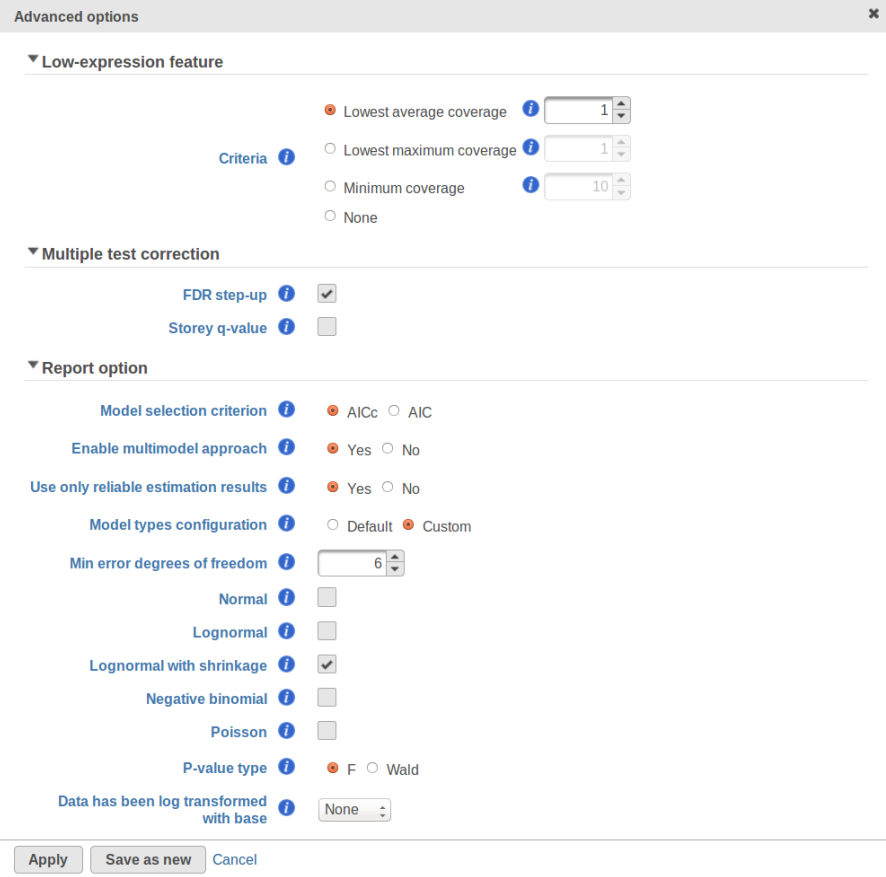
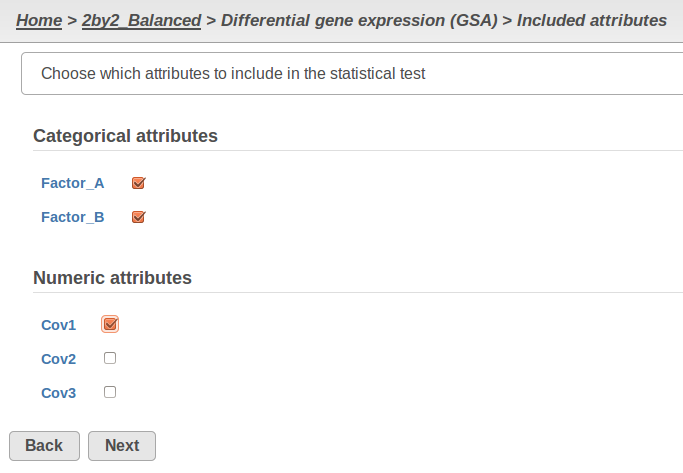
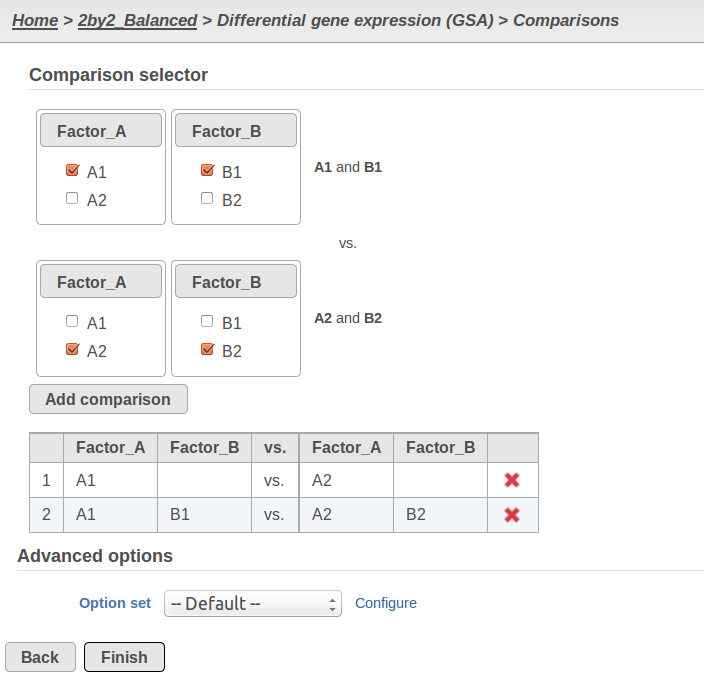
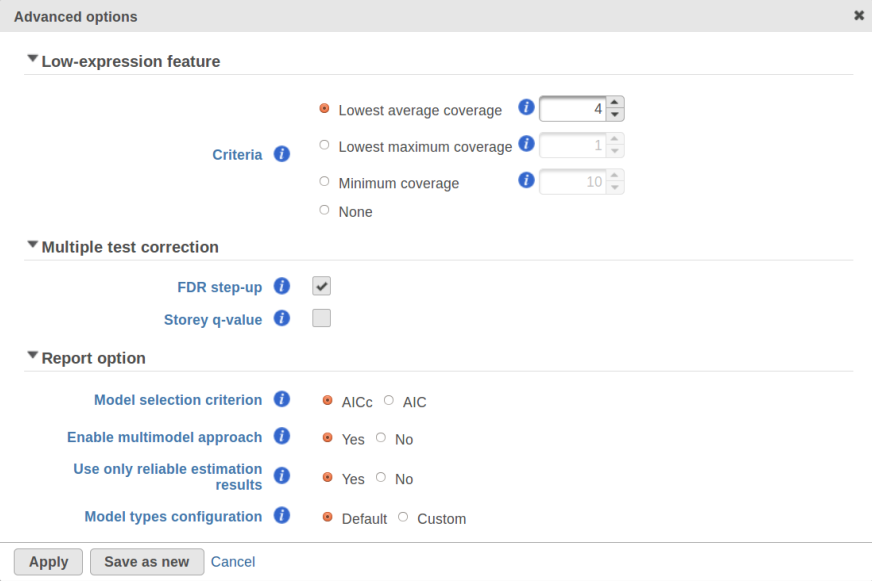
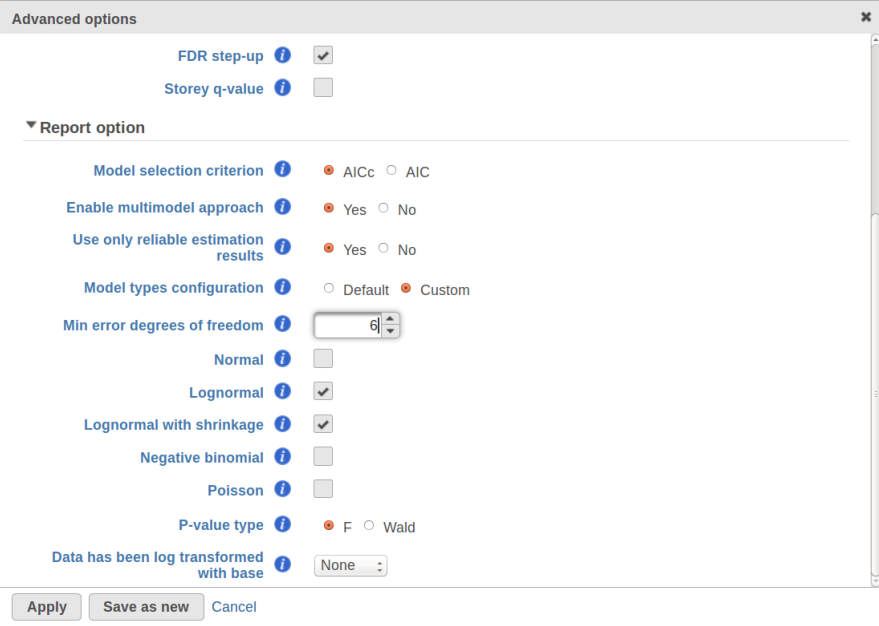
Currently, GSA is capable of considering the following five response distributions: Normal, Lognormal, Lognormal with shrinkage, Negative Binomial, Poisson (Figure 1). The GSA interface has an option to restrict this pool of distributions in any way, e.g. by specifying just one response distribution. The user also specifies the factors that may enter the model (Figure 2A) and comparisons for categorical factors (Figure 2B).

A) Choosing factors (attributes) in GSA

B) Choosing comparisons in GSA

Figure 2.

Based on the set of user-specified factors and comparisons, GSA considers all possible designs with the following restrictions:

1. It should be possible to estimate the specified comparison(s) using the design. That is, if the user specifies a comparison w.r.t levels of a certain factor, that factor must be included.
2. The design can include the factor interactions, but only up to 2^nd order.
3. If a 2^nd order interaction term is present in the design, then all first order terms must be present.

Restrictions 2 and 3 mean that GSA considers only hierarchical designs of 1^st and 2^nd order.

Example. Suppose the study involves two categorical factors, A and B. Factor A has two levels, and so does factor B. There are three observations for each combination of the levels of A and B, i.e. we are dealing with 2*2 design with 3 observations per cell, and the total sample size of 12. The user considers factor A to be of interest, and factor B is believed to be a nuisance factor, so a comparison is specified only w.r.t. factor A. As a result, the design space contains the following four elements:

A (main effect of A)
A + B (both main effects)
A + B + A*B (both main effects and the interaction of A and B)

In addition, the design pool can be restricted by the user through specifying the minimal number of degrees of freedom for the error (Figure 1). The recommended threshold value is six [1]. In this example, the largest model with both main effects and interactions has eight error degrees of freedom, hence all of the three possible designs will be considered. If the user decides to search for the best gene-specific model across all five possible response distributions, it amounts to fitting 3 * 5 = 15 models for each feature.

What model is the best for a given feature is determined through an information criterion specified by the user. At this point, the user can choose between AICc and AIC (Figure 1). AICc and AIC are recommended for small and medium sample sizes, correspondingly [2]. As the sample size goes up, AICc converges to AIC. Therefore, the user should usually do fine by utilizing the default choice, AICc.

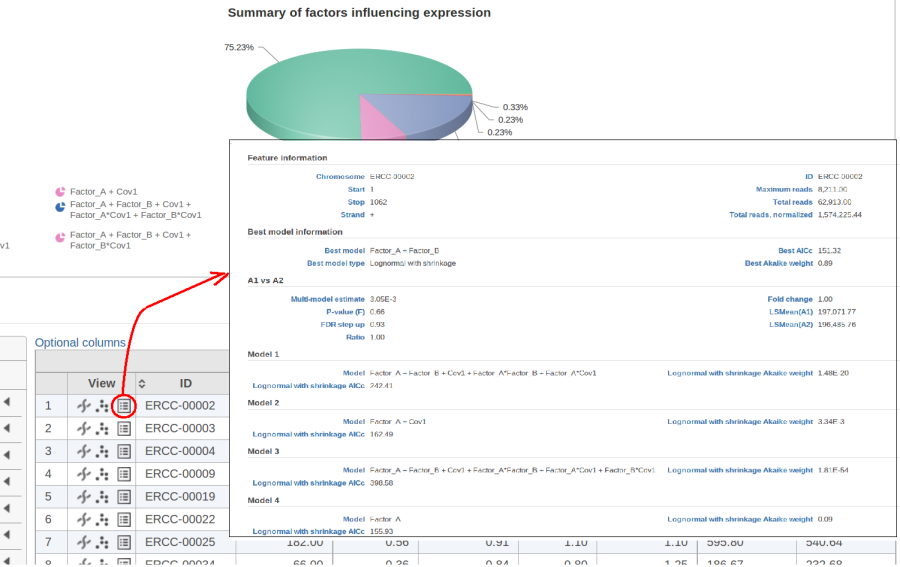
The model with the lowest information criterion is considered the best choice. It is possible to quantify the superiority of the best model by computing the so-called Akaike weight (Figure 3).The model's weight is interpreted as the probability that the model would be picked as the best if the study were reproduced. In the example above, we can obtain 15 Akaike weights that sum up to one. For instance, if the best model has Akaike weight of 0.95, then it is very superior to other candidates from the model pool. If, on the other hand, the best weight is 0.52, then the best model is likely to be replaced if the study were reproduced. We can still use this "best shot" model for downstream analysis, keeping in mind that that the accuracy of this "best shot" is fairly low.

Figure 3. For each feature, Akaike weights and other statistics are available via "View extra details report" button

Obtaining reproducible results in GSA

GSA is a great tool for automatic model selection: the user does not have to spend time and effort on picking the best model by hand. In addition, GSA allows one to run studies with no replication (one sample per condition) by specifying Poisson distribution in Advanced Options (Figure 1). However, not having enough replication is likely to deliver the results that are far more descriptive of the dataset at hand rather than the population from which the dataset was sampled. For instance, in the example from the previous section the number of fitted models (15) exceeds the number of observations (12), and therefore the results are unlikely to be representative of the population. If the study were to be reproduced with some 12 new samples, the list of significant features could be very different.

The problem is especially pronounced if the user disables the multimodel approach option in Advanced Options (Figure 1, "Enable multimodel approach"). In that case, for each feature only one model with the the highest Akaike weight is used. Under a low replication scenario and a large number of candidate models in the pool, such single best model provides a great description of the sampled data but not of the underlying population. The multimodel approach has some protection against generating non-reproducible results: all other things being equal, the p-value for the comparison of interest goes up as the number of models in the pool increases. Suppose there are two models with Akaike weights 0.5 each. When used separately, the first model generates a p-value of 0.04 and the second model generates p-value of 0.07. When multimodel inference is enabled it is possible to get a multimodel p-value well above 0.07. That protects one from making spurious calls but, if the number of models is very large, the user can end up with inflated p-values and no features to call.

The settings used in GSA's Default mode ("Model type configuration" in Figure 1) are aimed at ensuring higher reproducibility of the study for a fairly typical scenario of low replication. First of all, the response distribution is limited to "Lognormal with shrinkage". The latter is virtually identical to "limma trend" method from the limma package [5]. The idea behind shrinkage is to pool information across all of the genes which results in a more reproducible study under a low replication scenario. As the sample size goes up, the amount of shrinkage is reduced automatically, and eventually the method and its results become equivalent to a feature-specific "Lognormal" method (Figure 1).

Second, the error degrees of freedom threshold in Default mode is adjusted automatically for the purpose of excluding designs that have too many terms compared to the number of observations. Third, the hierarchical design restriction explained in the previous section is also aimed at keeping the number of considered designs reasonable. The user can override the first two restrictions by switching from Default to Custom mode in Advanced Options (Figure 1). The 2^nd order and hierarchical design restrictions cannot be disabled in GSA but they are absent in Flow ANOVA. The latter is similar to "Lognormal" option in GSA.

Using shrinkage plots

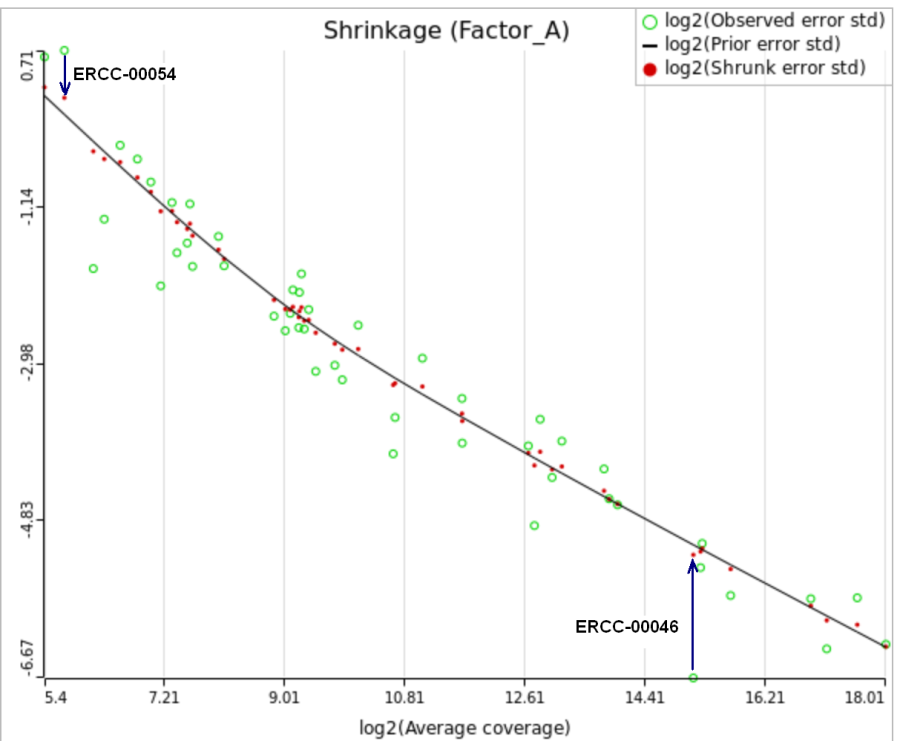
When "Lognormal with shrinkage" is enabled, a separate shrinkage plot is displayed for each design (Figure 4). First, a lognormal linear model is fitted for each gene separately, and the standard deviations of residual errors are obtained (green dots in the plot). Applying shrinkage amounts to two more steps. We look at how the errors change depending on the average gene expression and we estimate the corresponding trend (black curve). Finally, the original error terms are adjusted (shrunk) towards the trend (red dots). The adjusted error terms are plugged back into the lognormal model to obtain the reported results such as p-value.

 

All other things being equal, the comparison p-value goes up as the magnitude of error term goes up, and vice-versa. As a result, the "shrunken" p-value goes up (down) if the error term is adjusted up (down). Table 1 reports some results for two features highlighted in Figure 4

Figure 5. After shrinkage is applied, p-values are adjusted in the same direction as the corresponding error terms.

For a large sample size, the amount of shrinkage is small, (Figure 5), and the "Lognormal" and "Lognormal with shrinkage" p-values become virtually identical.

Figure 6. Shrinkage plot for a two group study with about 40 samples per group. Thanks to a large sample size, the error terms have almost no adjustment (green and red dots almost coincide)

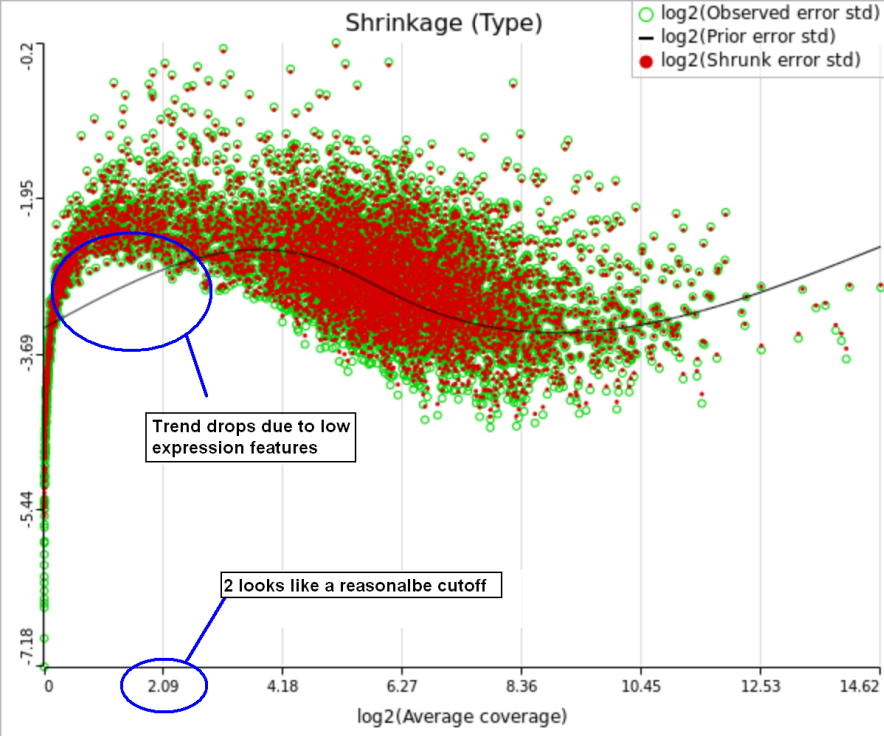
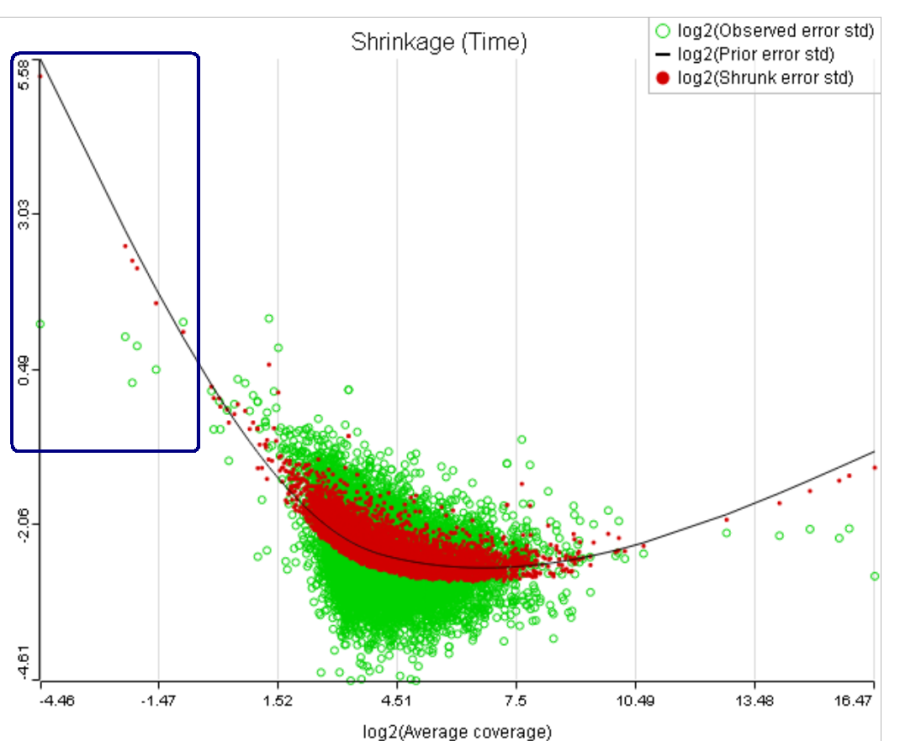
One important usage of the shrinkage plot is a meaningful setting of low expression threshold in Low expression filter section (Figure 6). For features with low expression, the proportion of zero counts is high. Such features are less likely to be of interest in the study, and, in any case, they cannot be modeled well by a continuous distribution, such as Lognormal. Note that adding a positive offset to get rid of zeros does not help because that does not affect the error term of a lognormal model much. A high proportion of zeros can ultimately result in a drop in the trend in the leftmost part of the shrinkage plot (Figure 6).

A rule of thumb suggested by limma authors is to set the low expression threshold to get rid of the drop and to obtain a monotone decreasing trend in the left-hand part of the plot.

Figure 7. A meaningful value for "Lowest average coverage" threshold can be easily determined based on the shrinkage

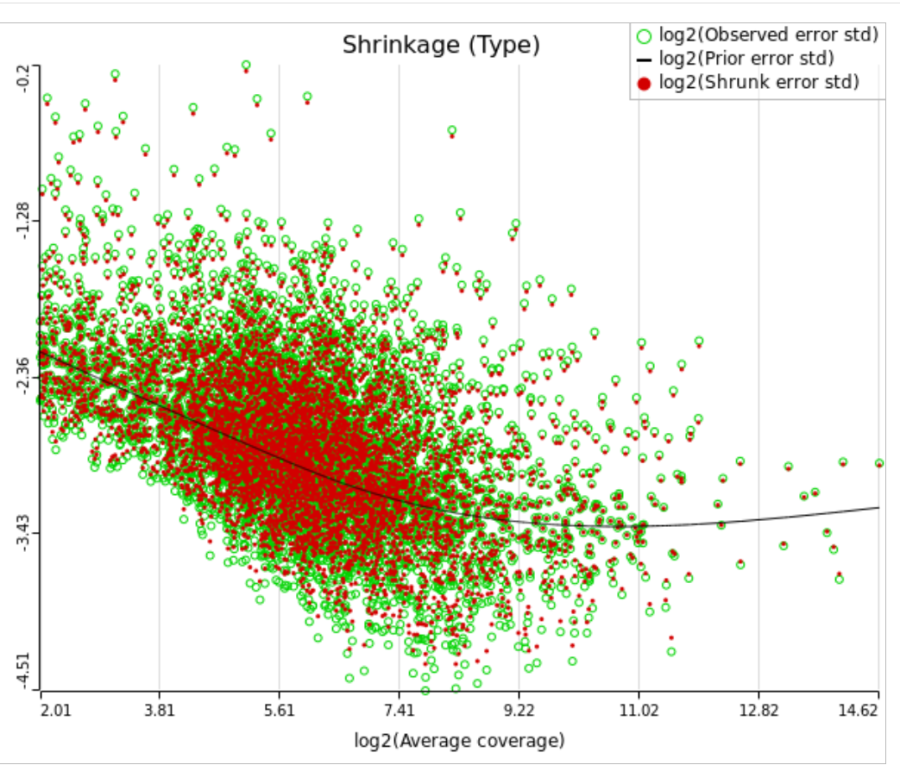
For instance, in Figure 5 it looks like a threshold of 2 can get us what we want. Since the x axis is on the log2 scale, the corresponding value for "Lowest average coverage" is 2^2=4 (Figure 6). After we set the filter that way and rerun GSA (Figure 7), the shrinkage plots takes the required form (Figure 8).

Figure 8. After resetting "Average coverage" threshold to 4 (Figure 6), the left part of shrinkage plot displays the desirable monotone decreasing trend. Note that the left boundary on the x axis becomes log2(4) = 2

Note that it is possible to achieve a similar effect by increasing a threshold of "Lowest maximal coverage", "Minimum coverage", or any similar filtering option (Figure 7). However, using "Average coverage" is the most straightforward: the shrinkage procedure uses log2(Average coverage) as an independent variable to fit the trend, so the x axis in the shrinkage plot is always log2(Average coverage) regardless of the filtering option chosen in Figure 7.

As suggested above, Lognormal with shrinkage is not intended to work for a dataset that contains a lot of zeros, a set of low expression features being one example. In that case, a count-based (Poisson or Negative Binomial) model is more appropriate. With that in mind, it appears to be a simple solution to enable Poisson, Negative Binomial, and Lognormal with shrinkage in Advanced Options and let the model selection happen automatically. However, there are a couple of technical difficulties with that approach. First, shrinkage can fail altogether because of the presence of low expression features (in that case, the user will get an informative error message in GSA). Second, there is an issue of reproducibility discussed above. However, for a large sample size shrinkage becomes all but disabled and reproducibility is not a concern. In that case, one can indeed cover all levels of expression by using Poisson, Negative Binomial, and Lognormal together.

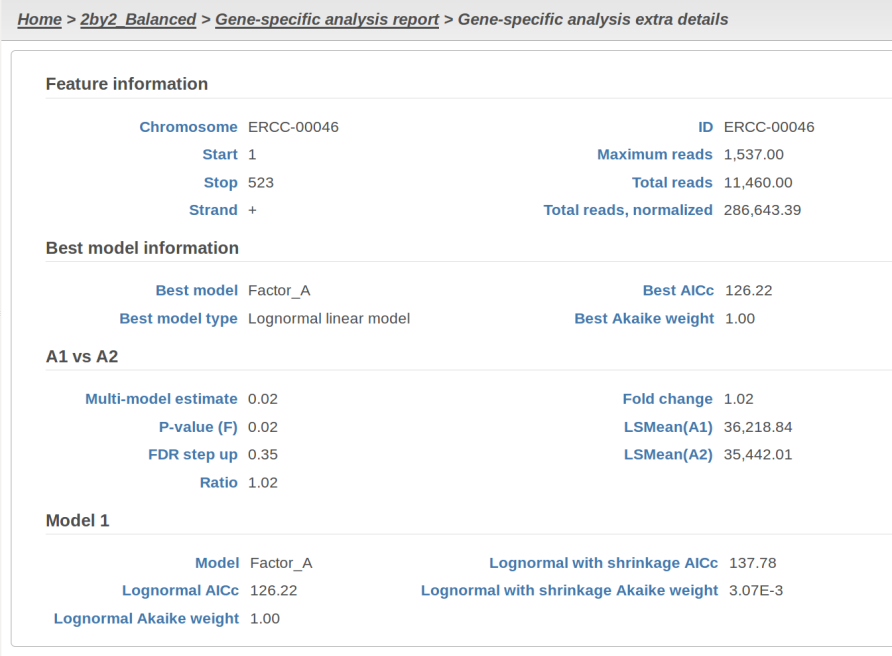
While shrinkage is likely to be beneficial for a small sample study overall, there can be some features that deviate so much from the rest that for them a feature-specific model can generate results that are more reproducible. The shrinkage plot provides a visually appealing, if informal, way to identify such features. For instance, in Figure 4 for feature ERCC-00046 the feature-specific error term (green) is far away from the trend and, as a result, it is adjusted upwards a lot. When the adjusted error term is plugged into the lognormal model for ERCC-00046, the model fits far worse for the observed ERCC-00046 counts, but the hope is that the results become closer to how ERCC-00046 behaves in the population. However, in this case the adjustment is quite big and one can say that a very large feature-specific effect is present and, as a result, shrinkage will do more harm than good.

A similar problem is present in count-based models as well. For instance, the handling of features with atypical variance parameters is addressed in DESeq2 [6], if in a rather peculiar manner. In DESeq2, if a feature has a variance that is "too high" compared to the trend then shrinkage is disabled altogether, which results in a much higher reported p-value because the variance is not adjusted downwards. However, for a feature with abnormally low variance shrinkage is never disabled which inflates the corresponding p-value because the variance is adjusted upwards. It is not clear why low and high variance features are not treated in the same manner, unless the goal is to exclude them from the final call list by inflating their p-values through this ad hoc procedure. One of DESeq2 authors admitted that, indeed, the goal is to stay on the "conservative side" when dealing with outlying features in a low replication scenario [7].

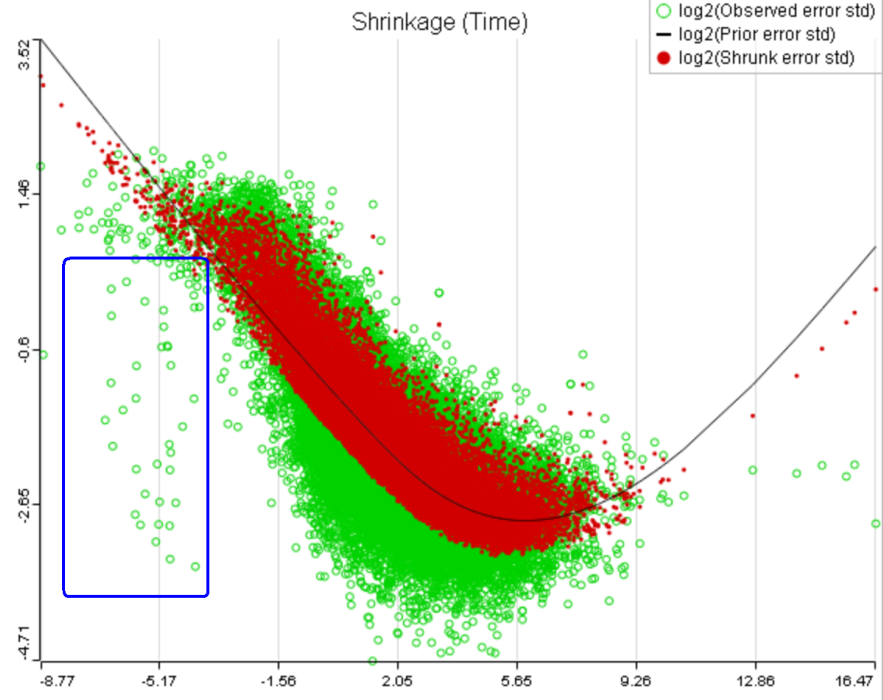
That line of reasoning suggests that neither DESeq2 nor limma are perfectly equipped for dealing with abnormal features. In fact, "limma trend" has no way to deal with them at all: shrinkage is applied regardless. If such abnormality is coupled with a low level of expression, it could be a good idea to get rid of the outlying features by raising the low expression threshold. For instance, while the trend in Figure 8A is monotone and decreasing in the left hand part of the plot, there are many low expression features with abnormally low error terms. Unless we have a special interest in those features, it makes sense to raise the low expression threshold so as to get rid of them.

A) Average expression threshold can be raised to get rid of low expression features with abnormal error terms, circled in blue

B) Six low expression features (circled in blue) account for a very sharp increase in the trend which can have an unduly large effect on overall results

Figure 9.

There can also be a situation where a small number of low expression features have a very high influence on the trend which affects the p-values for all of the features (Figure 8B). It is reasonable to assume that the overall results should not be sensitive to the presence or absence of a few features, especially if they happen to have low expression. It makes sense to get rid of such influential points by increasing the threshold accordingly.

Speaking of higher expression features, presently GSA has no automatic method to separate "abnormal" and "normal" features, so the user has to do some eyeballing of the shrinkage plot. However, for the purpose of investigating standalone outliers GSA can quantify the benefit of shrinkage in a well grounded way. In order to do that, one can enable both Lognormal and Lognormal with shrinkage in Advanced Options (Figure 9).

Figure 10. To quantify the benefit of shrinkage for any particular feature, enable these two models in "Custom" mode.

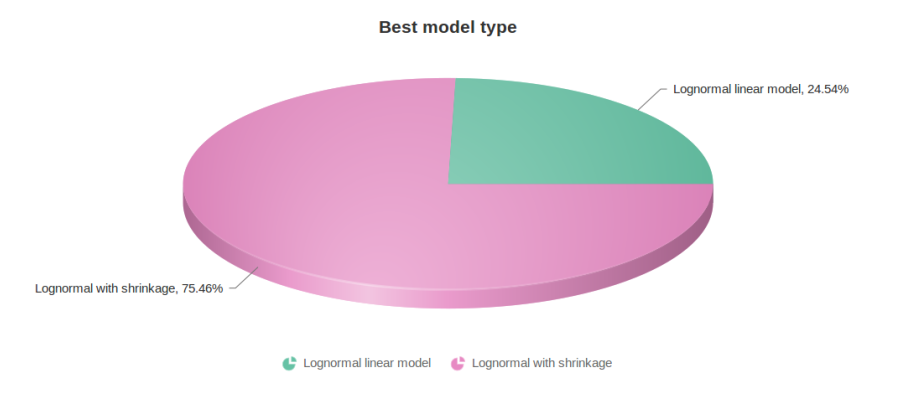
Figure 10 contains a pie chart for the dataset whose shrinkage plot is displayed in Figure 4. Because of a small sample size (two groups with four observations each) we see that, overall, shrinkage is beneficial: for an "average" feature, Akaike weight for feature-specific Lognormal is 25%, whereas Lognormal with shrinkage weighs 75%.

At the same time, if we look at ERCC-00046 specifically (Figure 11) we see that Lognormal with shrinkage fits so bad that its Akaike weight is virtually zero, despite having fewer parameters than feature-specific Lognormal.

Figure 12. For ERCC-00046, feature specific Lognormal model is dominant and shrinkage is the least likely to do well.

Using multimodel inference appears to be a better alternative to the ad hoc method in DESeq2 that switches shrinkage on and off all the way. Once again, it is both technically possible and emotionally tempting to automate the handling of abnormal features by enabling both Lognormal models in GSA and applying them to all of the transcripts. Unfortunately, that can make the results less reproducible overall, even though it is likely to yield more accurate conclusions about the drastically outlying features.

References

[1] Auer, 2011, A two-stage Poisson model for testing RNA-Seq.
[2] Burnham, Anderson, 2010, Model selection and multimodel inference.
[3] Dillies et al, 2012, A comprehensive evaluation of normalization methods.
[4] Storey, 2002, A direct approach to false discovery rates.
[5] Law et al, 2014, Voom: precision weights unlock linear model analysis. Note that this paper introduces both "limma trend" and "limma voom", but the present implementation in GSA corresponds to "limma trend".
[6] Love et al, 2014, Moderated estimation of fold change and dispersion for RNA-Seq data with DESeq2.
[7] Bioconductor support forum. Accessed last: 4/12/16. https://support.bioconductor.org/p/80745/#80758

Your Rating:

Thanks for voting!

Please Wait

Results:

64

rates